数据结构

小徐 Lv1
  2023-08-18 18:23:36 2023-08-18 18:23:36 创建   2023-09-08 15:04:09 2023-09-08 15:04:09 更新      3.7k 字  16 分钟  

绪论

数据结构的基本概念

基本概念和术语

数据：是信息的

数据对象：是具有相同性质的数据元素的集合，是数据的一个子集

数据结构三要素

  • 逻辑结构
    • 线性结构
    • 线性结构
      • 树形结构
      • 图形结构
  • 数据运算
  • 存储结构
    • 顺序存储
    • 链式存储
    • 索引存储
    • 散列存储

总结：

  • 数据的逻辑结构独立于其存储结构
  • 数据的存储结构是逻辑结构在计算机上的映射，它不能独立于逻辑结构而存在

算法

算法是问题求解步骤的描述

程序 = 数据结 + 算法

算法五个特性：

  1. 有穷性
  2. 确定性
  3. 可行性
  4. 零个或者多个输入
  5. 一个或者多个输出

算法的效率

  • 空间
  • 时间

算法时间复杂度

记忆公式：常对幂指阶

时间复杂度
时间复杂度

计算上述算法的时间复杂度T(n):
设最深层循环的语句频度(总共循环的次数)为x，则
由循环条件可知，循环结束时刚好满足在2^x>n

最好情况:元素n在第一个位置 –最好时间复杂度T(n)=0(1)
最坏情况:元素n在最后一个位置 –最坏时间复杂度T(n)=O(n)
平均情况:假设元素n在任意一个位置的概率相同为1/n –平均时间复杂度T(n)=O(n)
循环次数写

空间复杂度

空间规模与n没有关系的话S(n) = O(1) 算法原地工作——算法所需内存空间为常量

线性表

线性表是具有相同数据类型的n (n≥0) 个数据元素的有限序列，其中n为表长，当n= 0时线
性表是一个空表。

顺序表

顺序表的定义

线性表的顺序存储称为顺序表。把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关
系由存储单元的邻接关系来体现。

c语言求数据元素大小？

1
sizeof(ElemType)  //eg:sizeof(int) = 4B
  • 静态分配
1
2
3
4
5
6
7
#include <bits/stdc++.h>
#define MaxSize 10
//定义最大长度
typedef struct{
	int data[MaxSize];//用静态的“数组”存放数据元素
	int length;//顺序表的当前长度
}SqList;//顺序表的类型定义
  • 一维数组在静态分配时，由于数字的大小和空间已经固定，一旦空间占满，再加入新的数据就会产生溢出，进而导致程序崩溃。

  • 动态分配

    1
    2
    3
    4
    5
    6
    7
    #include<stdlib.h>
    #define InitSize 10  //顺序表的初始长度
    typedef struct{
    	int *data//动态分配数组指针
    	int length;//顺序表的当前长度
    	int Maxsize;//最大长度
    }SeqList;//顺序表的类型定义

    malloc函数
    malloc函数

顺序表的特点

  • 随机访问
  • 存储密度高
  • 拓展容量不方便
  • 插入、删除数据元素不方便

顺序表的基本操作

初始化

  • IintList(&L)

    • 静态初始

      1
      2
      3
      4
      5
      void InitList(SqList &L){
      	for(int i=0; i<MaxSize; i++)
      		L.data[i]=0;//将所有数据元素设置为默认初始值
      	L.length=0; //顺序表初始长度为0
      }

    • 动态初始

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      void InitList(SqList &L){
      	// 用malloc函数申请一片连续的存储空间
      	L.data = (int *)malloc(InitSize*sizeof(int));
      	L.length = 0;
      	L.MaxSize = InitSize;
      }
      //增加动态数组的长度
      Void IncreaseSize(SeqList &L,int len){
          int *p = L.data;
          L.data = (int *)malloc((L.MaxSize+len)*sizeof(int));
          for(int i =0;i<L.length;i++){
              L.data[i]=p[i]; // 将数据复制到新区域
          }
          L.MaxSize = L.MaxSize+len; //顺序表最大长度增加len
          free(p); // 释放原来的空间
      }

插入

  • bool ListInsert(SqList &L,int i,int e)
1
2
3
4
5
6
7
8
9
10
11
12
bool ListInsert(SqList &L,int i,int e){  
    if(i<1||i>L.length+1)
        return false;
    if(L.length>=MaxSize) // 空间已满
        return false;
	for(int j=L.length;j>=i;j--){
		L.data[j] = L.data[j-1];
	}
	L.data[i-1] = e;
	L.length++;
    return ture;
}

  • 时间复杂度: O(n)

  • 平均情况：假设新元素插入到任何一个位置的概率相同，即i= 1,2,3, … length+1 的概率都是p=
    1/(n+1)，i=1,循环n次; i=2时，循环n-1次; i=3， 循环n-2次….. i=n+1时，循环0次
    平均循环次数

删除

  • bool ListDelete(SqList &L,int i,int &e)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    bool ListDelete(SqList &L,int i,int &e){
    	if(i<1||i>L.length)
    		return false;
        e = L.data[i-1];
        for(int j =i;j<L.length;j++){
            L.data[j-1] = L.data[j];
        }
        L.length--;
        return true;
    }
    • 时间复杂度: O(n)
    • 平均情况：(n-1)/2

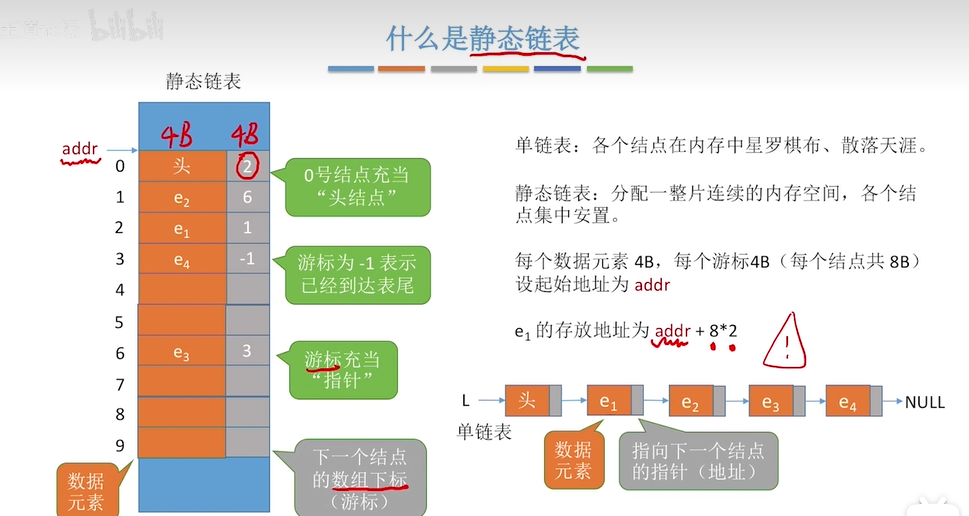
链表

链表的定义

1
2
3
4
typedef struct LNode{
    ElemType datd;
    struct LNode *next; // 指向下一个节点
}LNode,*LinkList;

表示一个单链表时，声明一个头指针L，指向单链表的第一个节点LNode *L;或者LinkList L;

强调这是一个单链表——LinkList

强调这是一个节点 ——LNode *

链表的基本操作

初始化

  • 不带头节点

    1
    2
    3
    4
    bool InitList(LinkList &L){
        L = NULL;
        return true;
    }

    • 带头节点

      1
      2
      3
      4
      5
      6
      7
      bool InitList(LinkList &L){
          L = (LNode *)malloc(sizeof(LNode));
          if(L==NULL) // 内存不足分配失败
              return false;
          L->next = NULL;
          return true;
      }

      空表判断：不带头节点：L==NULL

      ​ 带头节点：L->next ==NULL

插入

在第i个位置插入元素e

  • 带头节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    // 在第i个位置插入元素e   
    bool ListInsert(LinkList &L,int i,ElemType e){
        if(i<1)
            return false;
        LNode *p; // 指针p指向当前扫描到的节点
        int j =0; // 当前p指向是第几个节点
        p =L; 
        while(p!=NULL && j<i-1){
            p =p->next;
            j++;
        }
        if(p==NULL) // i值不合法
            return false;
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = e;
        s->next = p->next;
        p->next = s;
        return true;
    }

  • 不带头节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    // 在第i个位置插入元素e   
    bool ListInsert(LinkList &L,int i,ElemType e){
        if(i<1)
            return false;
        if(i==1){
            LNode *s = (LNode *)malloc(sizeof(LNode));
            s->data = e;
            s->next = L;
            L = s;
            retuen true;
        }
        LNode *p; // 指针p指向当前扫描到的节点
        int j =1; // 当前p指向是第几个节点
        p =L; 
        while(p!=NULL && j<i-1){
            p =p->next;
            j++;
        }
        if(p==NULL) // i值不合法
            return false;
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = e;
        s->next = p->next;
        p->next = s;
        return true;
    }

在p节点之前插入元素e

1
2
3
4
5
6
7
8
9
10
11
12
bool InsertPriorNode(LNode *p,ElemType e){
    if(p==NULL)
        return false;
    LNode *s = (LNode *)malloc(sizeof(LNode));
    if(s ==NULL)
        return false;
    s->next = p->next;
    p->next = s;
    s->data = p->data;// 将p节点元素复制在s中
    p->data = e;    
    return true;
}

删除

按位序删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool ListDelete(LinkList &L,int i,ElemType &e){
    if(i<1)
        return false;
    LNode *p;
    int j =0;
    p =L;
    while(p!=null && j<i-1){
        p = p->next;
        j++;
    }
    if(p==NULL)
        return false;
    if(p->next == NULL)
        return false;
    LNode *q = p->next; // q为被删除节点
    e = q->data;
    p->next = q->next;
    free(q);
    return trure;
}

删除指定节点 （移动值）

1
2
3
4
5
6
7
8
9
bool DeleteNode(LNode *p){
    if(p == NULL)
        return false;
    LNode *q = p->next;
    p->data = p->next->data;
    p->next = q->next;
    free(q);
    return true;
}

注意：如果p为最后一个节点会出现空指针异常

单链表的建立

尾插法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
LinkList List_Taillnsert(LinkList &L){
    int x;
    L = (LinkList)malloc(sizeof(LNode));
     L->next =NULL;//最好加上
    LNode *s,*r =L;
    scanf("%d",&x);
    while(x!=9999){
        s = (LNode*)malloc(sizeof(LNode));
        s->data = x;
        r->next =s;
        r=s; // r指向新的表尾节点
        scanf("%d",&x);
    }
    r->next = NUll;// 尾节点置空
    return L;
}

头插法

逆置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
LinkList List_Headlnsert(LinkList &L){
    int x;
    L = (LinkList)malloc(sizeof(LNode));
    LNode *s;
    L->next =NULL;//初始化空链表===》必须初始化 否则可能有脏数据
    scanf("%d",&x);
    while(x!=9999){
        s = (LNode*)malloc(sizeof(LNode));
        s->data = x;
        s->next =L->next;
        L->next=s; // r指向新的表尾节点
        scanf("%d",&x);
    }
    return L;
}

双链表

定义

1
2
3
4
5
typedef struct DNode{
    ElemType datd;
    struct DNode *next; // 指向下一个节点
    struct DNode *piror; // 指向下一个节点
}DNode,*DLinkNode;

插入

1
2
3
4
5
6
7
8
9
10
11
12
//p节点之后插入s节点
bool InsertNextDNode(DNode *p,DNode *s){
    if(p==NULL||s==NULL){
        return false;
    }
    s->next = p->next;
    if(p->next != NULL)// 如果p节点后面有节点
    	p->next->piror = s;
    s->piror = p ;
    p->next = s;
    return ture;
}

删除

1
2
3
4
5
6
7
8
9
10
11
12
13
// 删除p节点的后继节点
bool DeleteNextDNode(DNode *p){
    if(p==NULL)
        return false;
    DNode *q = p->next; //找到p的后继节点q
    if(q==NULL)
        return false; // p没有后继
    p->next = q->next; 
    if(q->next!=NUll) //q的节点不是最后一个节点
        q->next->prior = p;
    free(q);
    return ture;
}

循环链表

初始化

1
2
3
4
5
6
7
8
//初始化一个循环链表
bool InitList(LinkList &L){
    L = (LNode *) malloc (sizeof(LNode));
    if(L ==NULL)
        return false;
    L->next = L;// 头节点next指向头节点
    return ture;
}

静态链表

静态链表
静态链表

定义静态链表

1
2
3
4
5
#define MaxSize 10
struct Node {
    ElemType data;// 存储数据元素
    int next;//下一个元素的数组下标
}

栈

栈的定义

栈(Stack)是只允许在一端进行插入或删除操作的线性表

栈的特点

后进先出表

n个不同元素进栈，出栈元素不同排列的个数为

栈的基本操作

顺序栈

使用静态数组实现，并且需要记录栈顶指针

1
2
3
4
5
#define MaxSize 10
typedef struct{
    Elemtype data[MaxSize];
    int top; // 栈顶指针
}SqStack;

顺序存储:给各个数据元素分配连续的存储空间，大小为MaxSize * sizeof(ElemType)

初始
1
2
3
void InitStack(SqStack &s){
    S.top = -1;
}
进栈
1
2
3
4
5
6
7
bool Push(SqStack &S,ElemType x){
    if(S.top == MaxSize-1)
        return false;
    S.top++;
    S.data[S.top] = x;
    return true;
}
出栈
1
2
3
4
5
6
7
bool Pop(SqStack &S,ElemType &x){
    if(S.top == -1)
        return false;
    x=S.data[S.top];
    S.top--;
    return true;
}

链栈

1
2
3
4
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkStNode,*LiStack;
初始
1
2
3
4
void InitStack(LinkStNode *&s){
    s = (LinkStNode *)malloc(sizeof(LinkStNode));
    s->next =NULL;
}
入栈
1
2
3
4
5
6
7
8
bool Pup(LinkStNode *&s,int x){
    LinkStNode *p;
    p = (LinkStNode *)malloc(sizeof(LinkStNode));
    p->data = x;
    p->next = s->next;
    s->next  = p;
    return true;
}
出栈
1
2
3
4
5
6
7
8
9
10
bool Push（LinkStNode *&s,int &x）{
     LinkStNode *p;
    if(s->next == NULL)
        return false;
    p = s->next;
    x = s->data;
    s->next = p->next;
    free(p);
    return true;
}

栈的应用

括号匹配

思路分析
  graph TD;
      A[开始]-->B{还有未处理括号?};
      B-->|Yes|C[扫描下一个括号a];
      B-->|No|S{栈空?};
      S-->|No|G;
      S-->|Yes|su[匹配成功];
      su-->结束;
      C-->D{a是左括号?};
      D-->|Yes|E[a压入栈顶];
      E-->B;
      D-->|No|F{栈空};
      F-->|No|H[弹出栈顶元素b];
      H-->T{b与a匹配?};
      T-->|Yes|B;
      T-->|No|G;
      F-->|Yes|G[匹配失败];
      G-->结束;
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool brackCheck(char str[],int length){
    SqStack S;
    InitStack(S);
    for(int i=0;i<length;i++){
        if(str[i]=='('||str[i]=='{'||str[i]=='['){
            Push(S,str[i]);
        }else{
            if(StackEmpty(S)) // 栈空
                return false;
            char topElem;
            Pop(S,topElem);
            if(str[i]==')' && topElem!='('){
                return false;
            }
            if(str[i]=='}' && topElem!='{'){
                return false;
            }
            if(str[i]==']' && topElem!='['){
                return false;
            }
        }
    }
    return StackEmpty(S);
}

表达式求值

中缀表达式 后缀表达式 前缀表达式
运算符在两个操作数中间 运算符在两个操作数后面 运算符在两个操作数前面
a+b ab+ +ab
a+b-c ab+c- -+abc
a+b-c*d ab+cd*- -+ab*cd

中缀转化为后缀

初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。
从左到右处理各个元素，直到末尾。可能遇到三种情况:
①遇到操作数。直接加入后缀表达式。
②遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式，直到
弹出“(”为止。注意:“(” 不加入后缀表达式。
③遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式，
若碰到“(”或栈空则停止。之后再把当前运算符入栈。

按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。

队列

队列的定义

队列(Queue) 是只允许在一端进行插入，在另一端删除的线性表

队列的特点

先进先出表

队列的基本操作

循环队列

1
2
3
4
5
#define MaxSize 10
typedef struct{
    ElemType data[MaxSize];
    int front;rear;// 对头指针，队尾指针
}SqQueue;

判断队列已满条件

(Q.rear+1)%MaxSize == Q.front 对尾指针下一个就是对头

:warning:会牺牲一片存储空间

解决方法：

  1. 添加元素size判断个数
  2. 添加操作变量。删除时候tag=1，添加tag=0；队空 front=rear&&tag=1；

队列元素个数

（rear+MaxSize-front）%MaxSIze

初始
1
2
3
void InitQueue(SqQueue &Q){
	Q.rear=Q.front =0;
}
入队
1
2
3
4
5
6
7
8
bool EnQueue(SqQueue &Q,ElemType x){
    if((Q.rear+1)%MaxSize == Q.front)// 判断队满 
        return false;
    Q.data[Q.rear] =x;
   // Q.rear++; 这种当Q.rear =Q.front队列已经为空，但是Q.rear没有返回到0;
    Q.rear =(Q.rear+1)%MaxSize;
    return true;
}
出队
1
2
3
4
5
6
7
bool DeQueue(SqQueue &Q,ElemType &x){
    if(Q.rear ==Q.front){
        return false;
    }
    x = Q.data[Q.front];
    Q.front = (Q.front+1)%MaxSize;// 形成圈
}

链式队列

1
2
3
4
5
6
7
typedef struct LinKNode { //链式队列节点
    ElemType data;
    struct LinkNode *next;
}LinkNode;
typedef struct{ // 链式队列
    LinkNode *front，*rear; //队列的队头和队尾指针
}LinkQueue；
初始
1
2
3
4
void InitQueue(LinkQueue &Q){
    Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
    Q.front->next=NULL;
}
入队

  • 带头节点

    1
    2
    3
    4
    5
    6
    7
    void EnQueue(LinkQueue &Q,ElemType x){
        LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode));
        s->data = x;
        s->next = NULL;
        Q.rear->next = s; //新节点插入到rear之后 
        Q.rear = s; //修改尾指针
    }

  • 不带头节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void EnQueue(LinkQueue &Q,ElemType x){
        LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode));
        s->data = x;
        s->next = NULL;
        if(Q.front == NULL){ // 在空队列中插入第一个元素
            Q.front = s; //修改队头队尾指针
            Q.rear = s;
        }else{
            Q.rear->next = s; //新节点插入到rear之后 
        	Q.rear = s; //修改尾指针
        }
    }
出队

  • 带头节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    bool DeQueue(LinkNode &Q,ElemType &x){
        if(Q.front=Q.rear)
            return false; //空队
        LinkNode *p = Q.front->next;
        x=p->data;
        Q.front->next = p->next;
        if(Q.rear == p) // 此次是最后一个节点出队
            Q.rear = Q.front; //修改rear指针
        free(p);
        return true;
    }

  • 不带头节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    bool DeQueue(LinkNode &Q,ElemType &x){
        if(Q.front=Q.rear)
            return false; //空队
        LinkNode *p = Q.front;
        x=p->data;
        Q.front->next = p->next;
        if(Q.rear == p){
            Q.front = NULL;
        	Q.rear = NULL; 
        } // 此次是最后一个节点出队
        free(p);
        return true;
    }

特殊矩阵压缩存储

一维数组的存储结构

一维数组元素的存放地址

起始地址 LOC

数组元素a[i] =LOC+i*sizeof(ElemType)

二维数组的存储结构

  • 按行优先

二维数组按行优先，元素的存放地址

二维数组b[M] [N]]中起始地址 LOC

*数组元素b[i] [j]=LOC+(iN+j)sizeof(ElemType)*

  • 按列优先

二维数组按列优先，元素的存放地址

二维数组b[M] [N]]中起始地址 LOC

*数组元素b[i] [j]=LOC+(jM+i)sizeof(ElemType)*

按列优先
按列优先

  • 标题: 数据结构
  • 作者: 小徐
  • 创建于 : 2023-08-18 18:23:36
  • 更新于 : 2023-09-08 15:04:09
  • 链接: https://xiaoxua18.gitee.io/2023/08/18/数据结构/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
 评论
此页目录
数据结构
  1. 绪论
    1. 数据结构的基本概念
      1. 基本概念和术语
      2. 数据结构三要素
      3. 算法
        1. 算法时间复杂度
        2. 空间复杂度
  2. 线性表
    1. 顺序表
      1. 顺序表的定义
      2. 顺序表的特点
      3. 顺序表的基本操作
        1. 初始化
        2. 插入
        3. 删除
    2. 链表
      1. 链表的定义
      2. 链表的基本操作
        1. 初始化
        2. 插入
        3. 删除
      3. 单链表的建立
      4. 尾插法
      5. 头插法
    3. 双链表
      1. 定义
      2. 插入
      3. 删除
    4. 循环链表
      1. 初始化
    5. 静态链表
      1. 定义静态链表
    6. 栈
      1. 栈的定义
      2. 栈的特点
      3. 栈的基本操作
        1. 顺序栈
          1. 初始
          2. 进栈
          3. 出栈
        2. 链栈
          1. 初始
          2. 入栈
          3. 出栈
      4. 栈的应用
        1. 括号匹配
          1. 思路分析
          2. 算法实现
        2. 表达式求值
        3. 中缀转化为后缀
    7. 队列
      1. 队列的定义
      2. 队列的特点
      3. 队列的基本操作
        1. 循环队列
          1. 初始
          2. 入队
          3. 出队
        2. 链式队列
          1. 初始
          2. 入队
          3. 出队
  3. 特殊矩阵压缩存储
    1. 一维数组的存储结构
    2. 二维数组的存储结构